Jensen’s Inequality
Posted: Updated:
Jensen’s Inequality states that given a convex function \(f(x)\) and a random variable \(X\), then:
\[f(\mathbb{E}[X]) \leq \mathbb{E}[f(X)]\]In words:
The output of the average input is less than or equal to the average of the outputs.
Why is it true?
To answer this, we’ll nail down the starting point and determine the goal. We are given some convex function \(f(x)\) and a random variable \(X\) with a mean value of \(\mathbb{E}[X]\). We want to show \(f(\mathbb{E}[X])\) is less than something. Let’s represent this bare bones information with a bare bones visual:
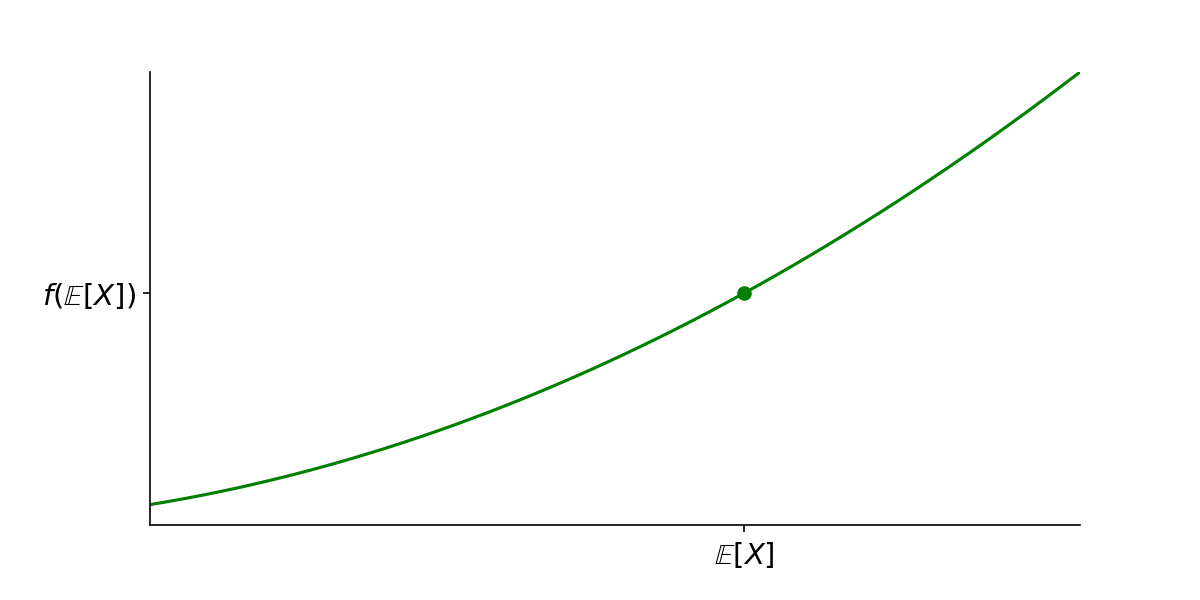The function \(f(x)\) with the point \((\mathbb{E}[X], f(\mathbb{E}[X]))\)
We may ignore which specific function this is because it ultimately won’t matter. All that matters is its convexity.
From here, we consider a function \(g(x)\) for which the relation holds with equality:
\[\mathbb{E}[g(X)] = g(\mathbb{E}[X])\]Specifically, we’ll use a linear function: \(g(x) = a + bx\) for some \(a\) and \(b\). Since the equality holds for any \(a\) and \(b\), we may choose them such that the line is tangent to \(f(x)\) at \((\mathbb{E}[X],f(\mathbb{E}[X]))\).
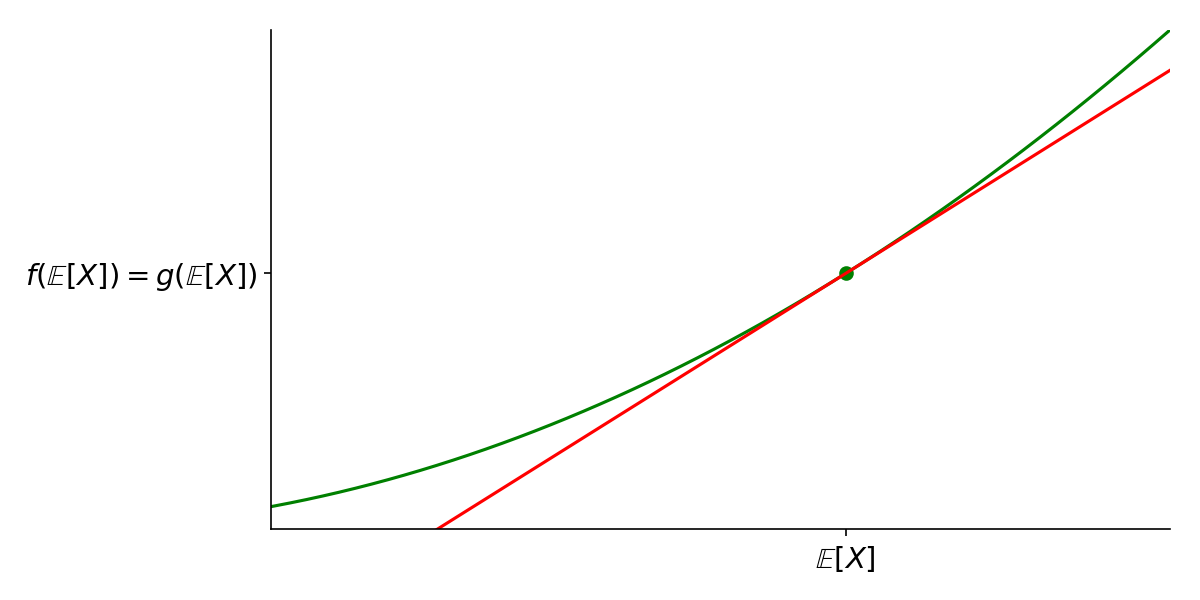The linear function \(g(x)\) chosen tangent to \(f(x)\) at \((\mathbb{E}[X], f(\mathbb{E}[X]))\)
Next, we’ll visualize the linear function, using colliding arrows to represent averaging:
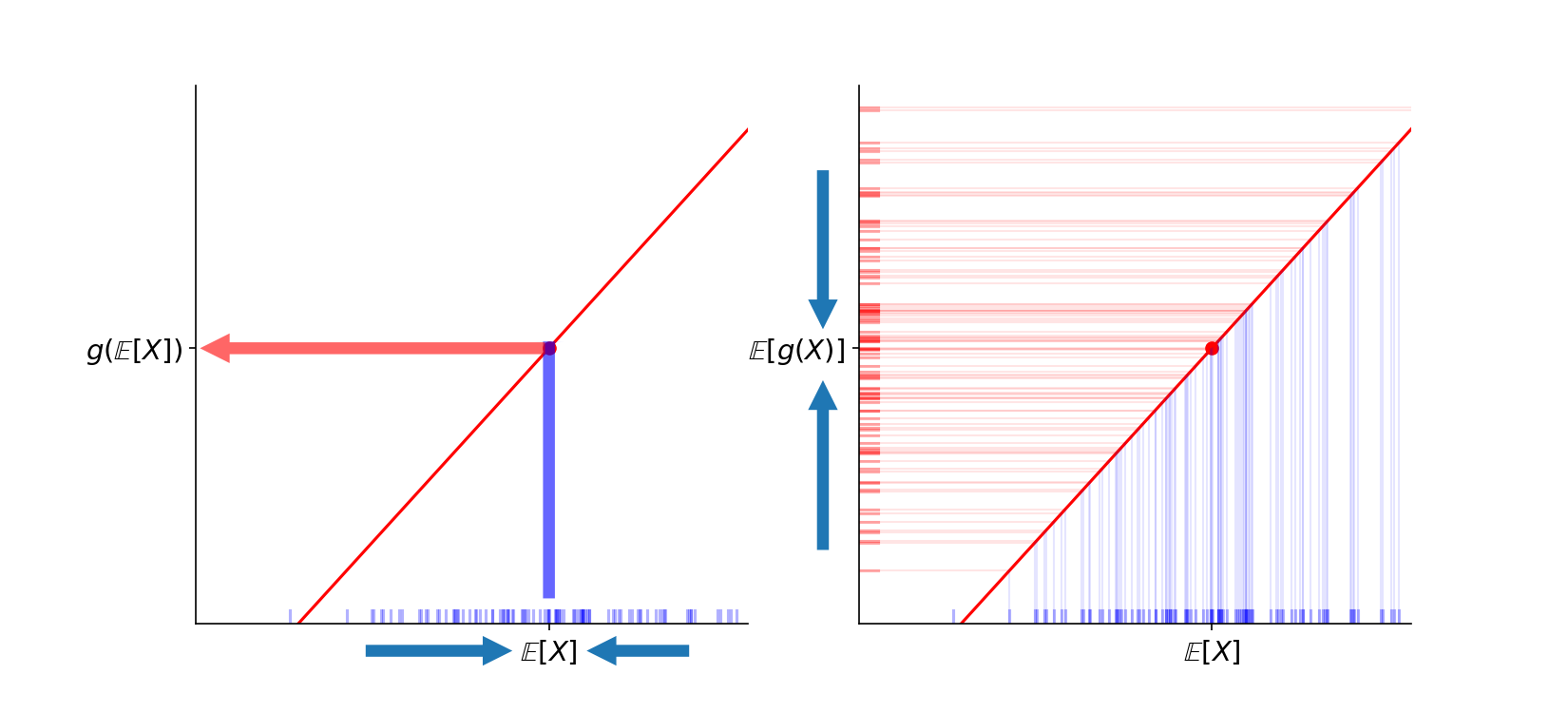Left: averaging \(X\) samples and passing the average to produce \(g(\mathbb{E}[X])\) \(\\\) Right: passing samples of \(X\) into \(g(x)\) and averaging the outputs to produce \(\mathbb{E}[g(X)]\)
On the left side, we see the computation for \(g(\mathbb{E}[X])\). On the right, we see it for \(\mathbb{E}[g(X)]\). Since \(g(x)\) is a linear function, we know these two arrive at the same number.
Next, imagine that on the right, we passed points through the \(f(x)\) instead of \(g(x)\). What would the effect be? Just trace the trajectory of a few samples:
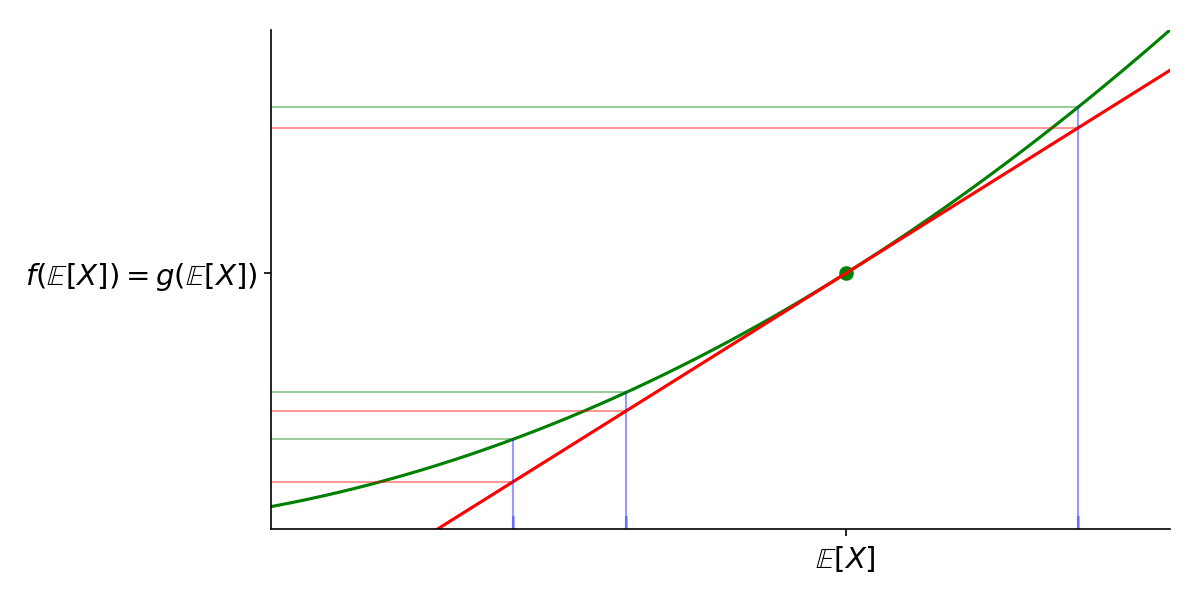If samples of \(X\) are passed to \(f(x)\) instead of \(g(x)\), outputs always increase.
No matter which \(X\) value is chosen, mapping to the convex function always yields a higher value than mapping to the linear function.
Now just for fun, we’ll pass them all through:
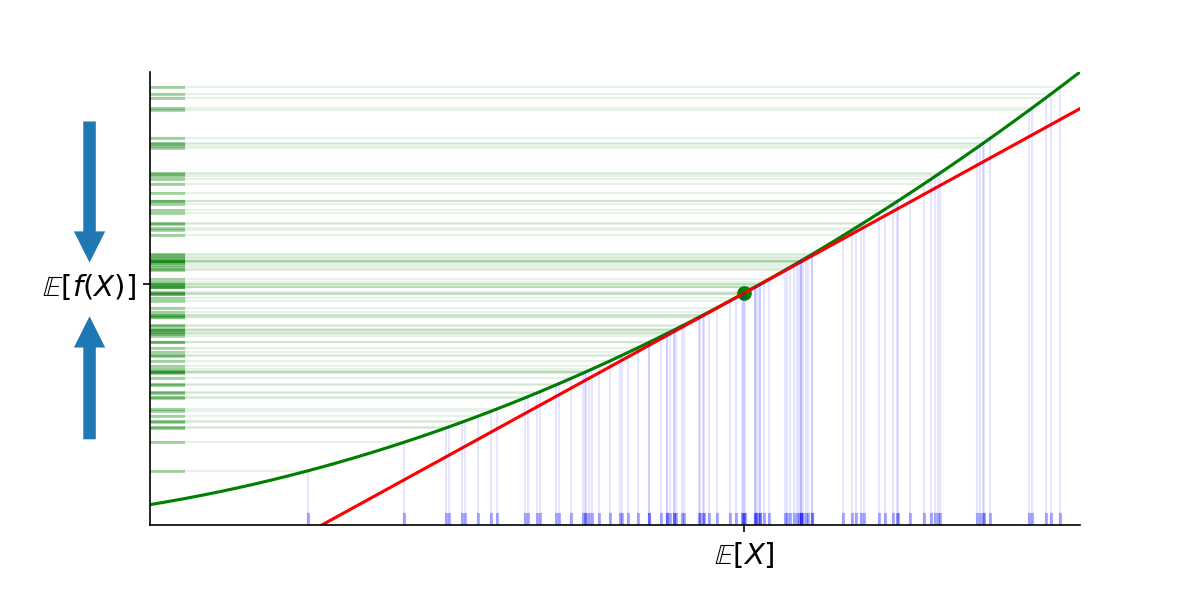
Since all the green outputs, the \(f(X)\)’s, must map to points above their respective red points, the \(g(X)\)’s, then we must have \(\mathbb{E}[g(X)] \leq \mathbb{E}[f(X)]\). Since \(\mathbb{E}[g(X)]=g(\mathbb{E}[X])=f(\mathbb{E}[X])\), then \(f(\mathbb{E}[X]) \leq \mathbb{E}[f(X)]\).
Intuition
My goal isn’t to provide a rigorous proof, but to communicate the feel as to why the inequality is true. In simplest terms, it’s because a convex function ‘bends off’ a linear function and that bending increases the output for all points. This understanding allows us to intuit a bit beyond the statement itself:
- By the same argument, the inequality is reversed for a concave function.
- The size of the difference \(\mathbb{E}[f(X)] - f(\mathbb{E}[X])\) increases as the variance of \(X\) increases or as the curvature of the convex function increases.
- There’s nothing special about the expectation operator, \(\mathbb{E}[\cdot]\). Any linear interpolation of points would respect the inequality.
As a general and unrelated note, this highlights the value of intuiting mathematics; it allows us to generalize one statement into others.
More Information
For another view of this argument, see my video on the topic.
References
Reference (3) is where the idea for the proof can be found. Chapter 3 of S. Boyd et al. (2004) and chapter 2 of MacKay (2003) provided useful context.
-
D. MacKay. Information Theory, Inference and Learning Algorithms. Cambridge University Press. 2003.
-
S. Boyd and L. Vandenberghe. Convex Optimization. Cambridge University Press. 2004.
-
Wikipedia contributors. Proof without words: Jensen’s Inequality. Wikipedia, The Free Encyclopedia.
Something to Add?
If you see an error, egregious omission, something confusing or something worth adding, please email dj@truetheta.io with your suggestion. If it’s substantive, you’ll be credited. Thank you in advance!